题目内容
（请给出正确答案）
若有两位候选人参选，并争夺n·51个选举人团(50个州和1个特区)的共计2m=538张选举人票，是否可能因两人恰好各得m=269张，而不得不重新选举？
a)试设计并实现一个对应的算法，并分析其时间复杂度;
b)若没有其它(诸如限定整数取值范围等)附加条件，该问题可否在多项式时间内求解？
如果结果不匹配，请 联系老师 获取答案
更多“考查如下问题：设s为一组共n个正整数，其总和为2m，判断是否…”相关的问题
问题描述:给定正整数序列x1,x2,…,xn要求:
①计算其最长递增子序列的长度s.
②计算从给定的序列中最多可取出多少个长度为s的递增子序列.
③如果允许在取出的序列中多次使用x1和xn,则从给定序列中最多可取出多少个长度为s的递增子序列.
算法设计:设计有效算法完成①、②、③提出的计算任务.
数据输入:由文件input.txt提供输入数据.文件第1行有1个正整数n,表示给定序列的长度.接下来的1行有n个正整数x1,x2,...,xn,
结果输出:将任务①、②、③的解答输出到文件output.txt.第1行是最长递增子序列的长度s.第2行是可取出的长度为s的递增子序列个数.第3行是允许在取出的序列中多次使用x1和xn时可取出的长度为s的递增子序列个数.
问题描述:子集和问题的一个实例为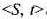
.其中,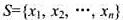
是一个正整数的集合,c是一个正整数.子集和问题判定是否存在S的一个子集S1,使得
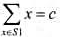.试设计一个解子集和问题的回溯法.
算法设计:对于给定的正整数的集合
和正整数c,计算S的一个了集S1,使得
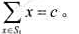
数据输入:由文件input.txt提供输入数据.文件第1行有2个正整数n和c,n表示S的大小,c是子集和的目标值.接下来的1行中,有n个正整数,表示集合S中的元素.
结果输出:将子集和问题的解输出到文件output.txt.当问题无解时,输出“NoSolution!".
问题描述:设磁盘上有n个文件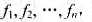
每个文件占用磁盘上的1个磁道.这n个文件的检索概率分别是
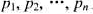且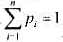
磁头从当前磁道移到被检信息磁道所需的时间可用这两个磁道之间的径向距离来度量.如果文件fi存放在第i(1≤i≤n)道上,则检索这n个文件的期望时间是
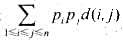.式中,d(i,j)是第i道与第j道之间的径向距离|i-j|.
磁盘文件的最优存储问题要求确定这n个文件在磁盘上的存储位置,使期望检索时间达到最小.试设计一个解此问题的算法,并分析算法的正确性与计算复杂性.
算法设计:对于给定的文件检索概率,计算磁盘文件的最优存储方案.
数据输入:由文件input.txt给出输入数据.第1行是正整数n,表示文件个数.第2行有n个正整数a,表示文件的检索概率.实际上第k个文件的检索概率应为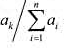
结果输出:将计算的最小期望检索时间输出到文件output.txt.
问题描述:设有n个顾客同时等待一项服务,顾客i需要的服务时间为ti(1≤i≤n).应如何安排n个顾客的服务次序才能使平均等待时间达到最小？平均等待时间是n个顾客等待服务时间的总和除以n.
算法设计:对于给定的n个顾客需要的服务时间,计算最优服务次序.
数据输入:由文件input.txt给出输入数据.第1行是正整数n,表示有n个顾客.接下来的1行中,有n个正整数,表示n个顾客需要的服务时间.
结果输出:将计算的最小平均等待时间输出到文件output.txt.
问题描述:给定有向图G=(V,E).设P是G的一个简单路(顶点不相交)的集合.如果V中每个顶点恰好在P的条路上,则称P是G的一个路径覆盖.P中路径可以从V的任何一个项点开始,长度也是任意的,特别地,可以为0.G的最小路径覆盖是G的所含路径条数最少的路径覆盖.
设计一个有效算法求一个有向无环图G的最小路径覆盖.
[设V={1,2,...,n},如下构造网络G1=(V1,E1):
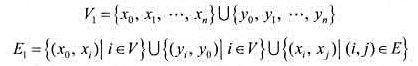
每条边的容量均为1.求网络G1的(x0,y0)最大流.]
算法设计:对于给定的有向无环图G,找出G的一个最小路径覆盖.
数据输入:由文件input.txt提供输入数据.文件第1行有2个正整数n和m.n是给定有向无环图G的顶点数,m是G的边数.接下来的m行,每行有2个正整数i和j,表示一条有向边(i,j).
结果输出:将最小路径覆盖输出到文件output.txt.从第1行开始,每行输出一条路径.文件的最后一行是最少路径数.
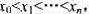处.居民们希望在城市中至少选择一个,但不超过k个居民点建立服务机构.在每个居民点xi处,服务需求量为wi≥0.在该居民点设置服务机构的费用为ci≥0.假设居民点xi到距其最近的服务机构的距离为di,则居民点x的服务费用为
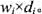建立k个服务机构的总费用为A+B.A是在k个居民点设置服务机构的费用的总和;B是n个居民点服务费用的总和.算法设计:对于给定直线上的n个点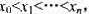
,计算在直线L上最多设置k处服务机构的最小总费用.
数据输入:由文件input,txt给出输入数据.第1行有2个正整数n和k.n表示直线L上有n个点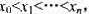k是服务机构总数的上限.接下来的n行中,每行有3个整数.第i+1行的3个整数xi、wi、ci,分别表示相应居民点的位置坐标、服务需求量和在该点设置服务机构的费用.
结果输出:将计算的最小服务费用输出到文件output.txt
算法设计:对于给定的树T,以及障碍物在树T中的分布情况,计算机器人从起点s到终点t的最少移动次数.
数据输入:由文件input.txt提供输入数据.文件的第1行有3个正整数n,s和t,分别表示树T的顶点数,起点s的编号和终点t的编号.
接下来的n行分别对应于树T中编号为0,1,...,n-1的项点.每行的第1个整数h表示顶点的初始状态,当h+1时表示该顶点为空顶点,当h=0时表示该顶点为满顶点,其中已有一个障碍物.第2个数k表示有k个顶点与该项点相连.接下来的k个数是与该顶点相连的顶点编号.
结果输出:将计算出的机器人最少移动次数输出到文件output.txt.如果无法将机器人从起点s移动到终点t,则输出“NoSolution!"
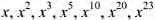.可以证明,计算x23最少需要6次乘法.计算x23的幂序列中各幂次1、2、3、5、10、20、23组成了一个关于整数23的加法链.一般情况下,计算xn的幂序列中各幂次组成正整数n的一个加法链:
上述最优求幂问题相应于正整数n的最短加法链问题,即求n的一个加法链,使其长度r达到最小.正整数n的最短加法链长度记为l(n).
算法设计:对于给定的正整数n,计算相应于正整数n的最短加法链.
数据输入:由文件input.txt给出输入数据.第1行有1个正整数n.
结果输出:将计算的最短加法链长度l(n)和相应的最短加法链输出到文件output.txt.
问题描述:给定一个赋权无向图G=(V,E),每个顶点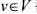
都有权值w(v).如果
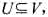,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
算法设计:对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最小权顶点覆盖.
数据输入:由文件input.txt给出输入数据.第1行有2个正整数n和m,表示给定的图G有n个顶点和m条边,顶点编号为1,2,...,n.第2行有n个正整数表示n个顶点的权.接下来的m行中,每行有2个正整数u和v,表示图G的一条边(u,v).
结果输出:将计算的最小权顶点覆盖的顶点权值和以及最优解输出到文件output.txt.文件的第1行是最小权顶点覆盖顶点权之和;第2行是最优解xi(1≤i≤n),xi=0表示顶点i不在最小权顶点覆盖中,xi=1表示顶点i在最小权顶点覆盖中.
设A={x|x∈R∧x≠0，1}。在A上定义6个函数如下：
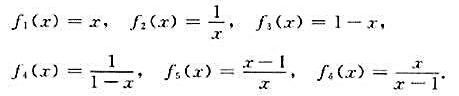
V=＜S，°＞，其中S={f1，f2，...，f6}，°为函数的复合.。
(1)给出V的运算表。
(2)说明V的幺元和所有可逆元素的逆元：
问题描述:现有n种不同形状的宝石,每种n颗,共n颗.同一种形状的n颗宝石分别具有n种不同的颜色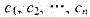
中的一种颜色.欲将这n2颗宝石排列成n行n列的一个方阵,使方阵中每行和每列的宝石都存n种不同形状和n种不同颜色.试设计一个算法,计算出对于给定的,有多少种不同的宝右排列方案.
算法设计:对于给定的n计算出不同的宝石排列方案数.
数据输入:由文件input.txt给出输入数据.第1行有1个正整数n(0＜n＜9).
结果输出:将计算的宝石排列方案数输出到文件output.txt.
